こんにちは。京都(宇治・伏見)のプロ家庭教師 内藤 睦です。
ブログにご訪問いただき、ありがとうございます。
私の自己紹介はこちらから☟クリックして頂くと詳細に続きます。

「基本問題は解けるのに、応用問題がなかなか解けない…」
そのようなお悩みをお持ちではありませんか?
受験生の方は、模試や過去問と向き合って、
余計にそんな気持ちを持たれるかもしれません。
まったく分からないわけではない。
基本問題はそれなりに解ける。
けど、ちょっとひねりの利いた問題が難しい…。
こういう場合、「自分には算数・数学のセンスがないんだ」と思うかもしれません。
今回から、私なりに考える原因を「スキル不足」「メンタル面」に分けて
何回かでお伝えしてきたいと思います。
①スキル編その1 計算力が足りていない ②スキル編その2 公式・定理が完璧に身に着いていない ③スキル編その3 問題状況をイメージできていない ④スキル編その4 問題状況を式で表せない ←今回はココ ⑤メンタル編その1 解けない算数・数学の問題はない ⑥メンタル編その2 正解を逆から導き出す気持ちが足りない ⑦メンタル編その3 センスの問題と思っている |
複雑な問題は、状況を式にあらわすのが難しい!
前回、「複雑な問題は、状況把握が難しい!」とお伝えしました。
前回の記事はコチラ
今回の「状況を式にあらわす」のは、その後です。
複雑な状況を把握した後は、
「問題文の条件や数字を式にする」をクリアしないといけません。
たとえば、「リンゴ1個の値段はミカン1個の値段の3倍です」
という状況は、
中学受験算数であれば
「ミカン1個の値段を①としたらリンゴ1個の値段は③で表せる」と考え、
中学数学であれば
「ミカン1個の値段を $x$ としたらリンゴ1個の値段は$3x$と表せる」となります。
ただ、これくらいなら簡単ですが、複雑な応用問題になればなるほど
表し方が難しいんですよね。
そして、中学受験算数と中学数学では、式の利用の使い方が少し変わります。
大きく言うと、
中学受験算数では、
問題文で与えられた状況を線分図や比の関係などで上手く表せれば、
式はほとんど書かずとも頭の中で答えまで導ける場合も多い。
が、
中学以降の数学では、状況をとにかく式にする力が大切。
なぜなら、$x$を立ててそれを求めるためには式が必要だから。
です。
たとえば、大小関係を表す時。
「キウイ1個の値段はミカン1個の値段より30円高いです。」であれば、
ミカン $x$円 キウイ $x$+$30$円
もしくは
キウイ $x$円 ミカン $x$-$30$円
のいずれかで表せる必要があるのはもちろんです。
それでは
「150円のリンゴと120円の柿を合わせて20個買いました。
ところが、リンゴの個数と柿の個数を逆に買ってしまったので、
予定より120円安くなりました。予定金額は何円ですか」
という問題があったらどう解くでしょうか。
順に説明していきましょう。
中学受験算数では、図や比のイメージがあれば式ができる
中学受験算数の場合、比を使うか図を使うことが大切です。
幾つか方法はありますが、こちらではこのような方法を紹介します。
まずは、「予定より安くなった」ということは、「予定より柿を多く買った」
ということを、問題文から把握します。
そして、リンゴと柿の個数が同じ部分と、違う部分を意識して図を描くのです。
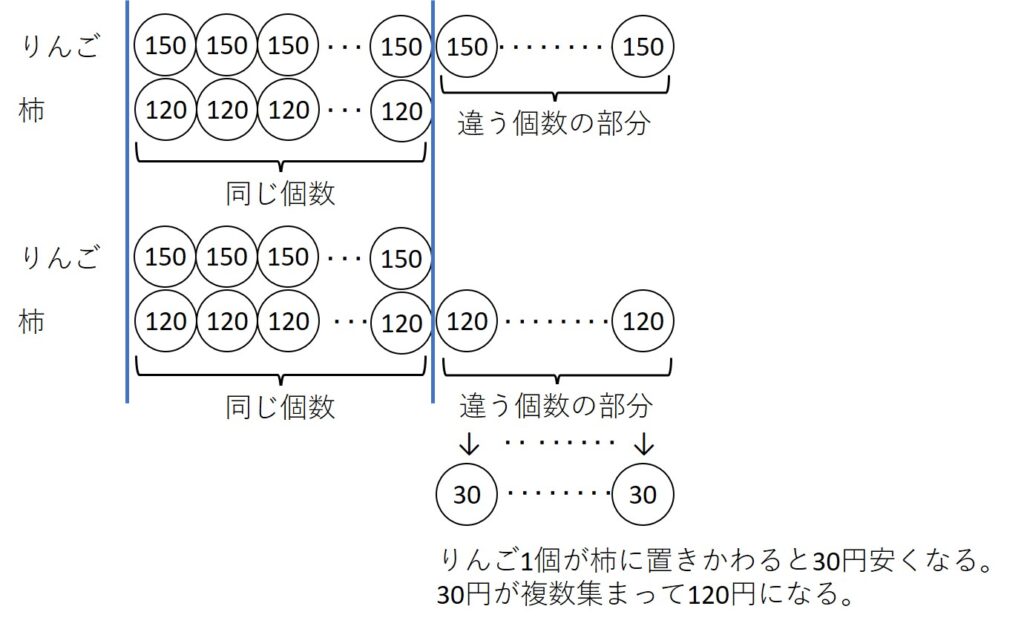
そうすると、リンゴが一つ柿におきかわると150円-120円=30円安くなり、
30円がいくつか集まって120円安くなった、と考えられます。
ということから、120÷30=4
と考えられ、リンゴの方が柿より4個多いとわかります。
今度は、リンゴの方が柿より4個多く、合計20個ある、ということを図にします。

そうすると、この図から(20-4)÷2=8、8+4=12
という式が思い浮かび、リンゴ12個、柿8個という答えがわかります。
そうすれば、あとは150×12+120×8=2760円 と答えが出ます。
中学数学は、式を立てる力が大事!
一方で、中学数学はとにかく式を作ることが大切です。
この場合、$x$だけを使う一次式でも、$x$と$y$を使う式、どちらでもよいでしょう。
(1) $x$だけを使う場合
リンゴを $x$個とおくと、柿は20-$x$個とおけます。
すると、予定では150円のリンゴ $x$ 個、120円の柿 20-$x$ 個買うことに。
実際には150円のリンゴ 20-$x$ 個、120円の柿 $x$ 個買ったら、120円安くなったので
150 $x$ +120 (20-$x$ )=150 (20-$x$)+120 (20-$x$) + 120
となります。
「120円安くなった」ということは、「予定金額より実際の金額は120円少ない」となり
「実際の金額に120円足すと予定金額になる」という意味です。
もちろん
150 $x$ +120 (20-$x$) -120 =150 (20-$x$)+120 (20-$x$)
でも構いません。
これを解くことで、$x$が出ます。
(2) $x$と $y$ 使う場合
リンゴを $x$個とおくと、柿は$y$個とおけます。
この場合、 $x$+$y$=20を式としておき、前回の式をつけて連立方程式として解きます。
いかがでしたか?
中学受験では、式だけでなく図やイメージと持つ力も大切になりますが、
どちらも式を作る力が大切です。
日本語の言葉や文法を理解して文章を読むのと同じように、
算数・数学の記号やルールを理解して式を作る。
この力をつけるのが大切です。
ご家庭に寄り添い、生徒さんの成長を共に支え、喜び合える。
そんな関係が築けたら幸いです。
気になることやご相談がありましたら、お気軽にご連絡ください。
お問い合わせ
☏電話でのお問い合わせ、
ご質問・ご相談はこちら
TEL.080-9895-5442
受付時間 / 9:30 – 21:00
※出られない場合は、折り返しお電話いたします
✉メールでのお問い合わせも受け付けています。










この記事へのコメントはありません。