こんにちは。京都(宇治・伏見)のプロ家庭教師 内藤 睦です。
ブログにご訪問いただき、ありがとうございます。
私の自己紹介はこちらから☟クリックして頂くと詳細に続きます。

今回は中学受験算数で差がつきやすい分野の一つ、
図形の面積比の考え方について書いていきます。
面積比は面積を求めるのと違う!どうすればいいの?
面積比を求める問題にはいくつかタイプがありますが、
砂時計型とかリボン形、チョウチョ型などの相似形の面積を比べるタイプの問題についてです。
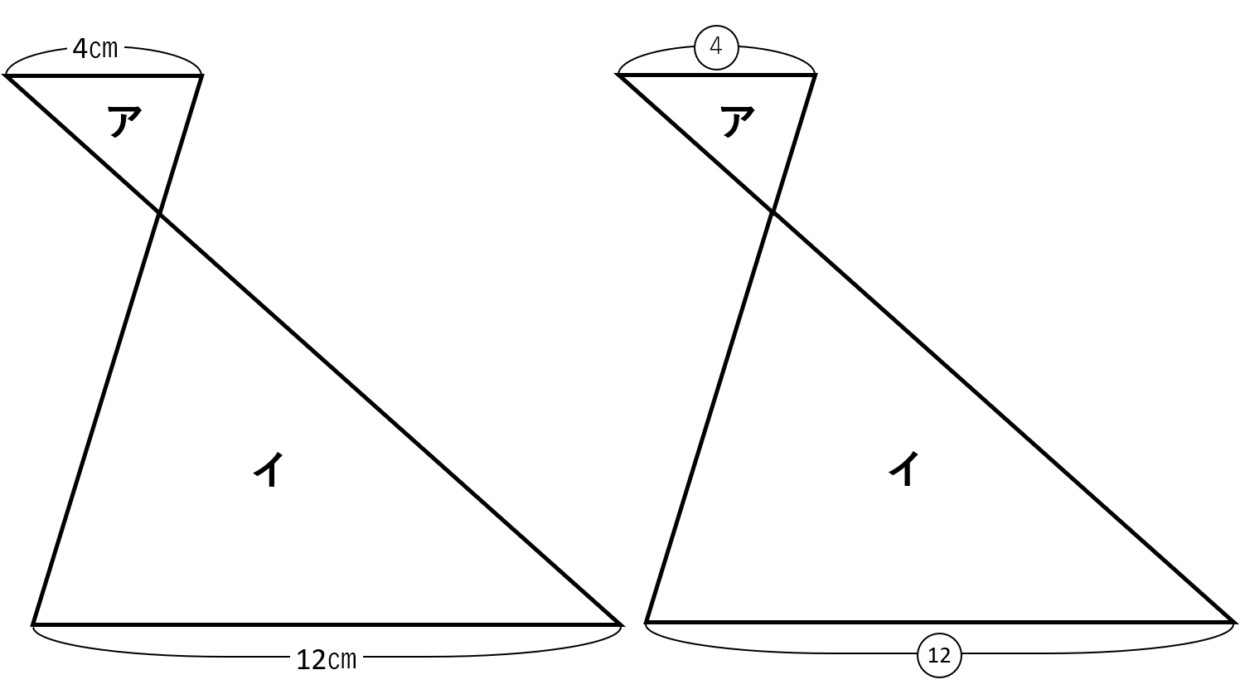
はい、こういう砂時計型とかリボン形、チョウチョ型なんて
呼ばれる形です。
左のように長さが具体的に書かれているものもありますが、
右のように比がわかっているだけの場合もあります。
こちらのアとイの面積比を考える時、
「辺の相似比の二乗で考えましょう」という説明が多いです。
具体的にはアとイの辺の長さの比はア:イ=$4:12$ = $1:3$
なので面積比はアは$1×1$、イは$3×3$、
つまりア:イ=$1:9$というものです。
でも、こういう考え方はいかがでしょうか?
上記の三角形と同じ小さなタイルを敷きつめて枚数を比べる、という考え方です。
ちょっと前に、「鬼滅の刃」の「善逸」の着物柄を使って
面積比の話をしました。
こういうやつですね。

一つの三角形の面積を1とすると、
辺の長さが2倍になると、面積は4倍になります。
これは同じ大きさの黄色と白の三角形が
4つ集まっていることからもわかりますね!
この考え方が、こういった面積比でも使えるんです!
アと同じ大きさのタイルを用意しましょう。

上記のタイルはアと同じ大きさです。
これを使ってイの図形に敷きつめると…。
こうなりました!

小さなタイル9枚分ですね。
そうなんです。辺の長さが3倍だから、タイルは3×3の9枚敷きつめられる。
つまり、ア:イの面積比は$1:9$ということになります。
いろんな面積は元となる小さなタイルの枚数で考えられる
それではちょっと別の問題です。
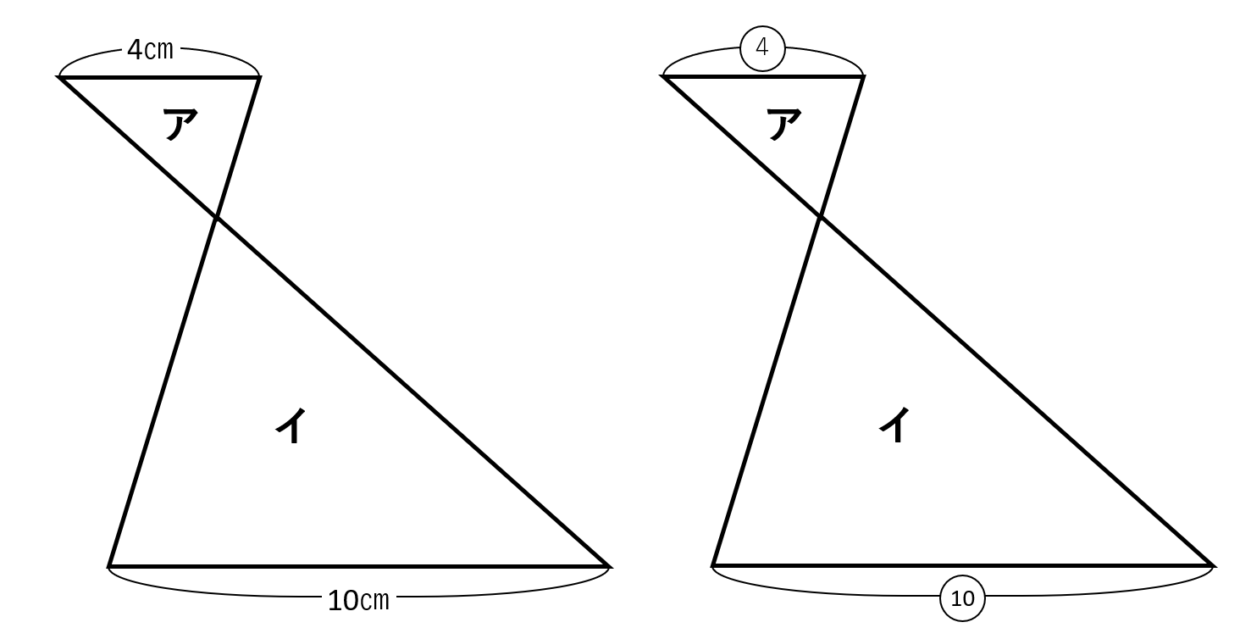
これはどう考えましょう?
アと同じ大きさのタイルが
いくつ敷きつめられるかを考えてもうまくいきません。
底辺の長さが4cmと10cmだから、比べにくいんですね。
どうしましょうか?
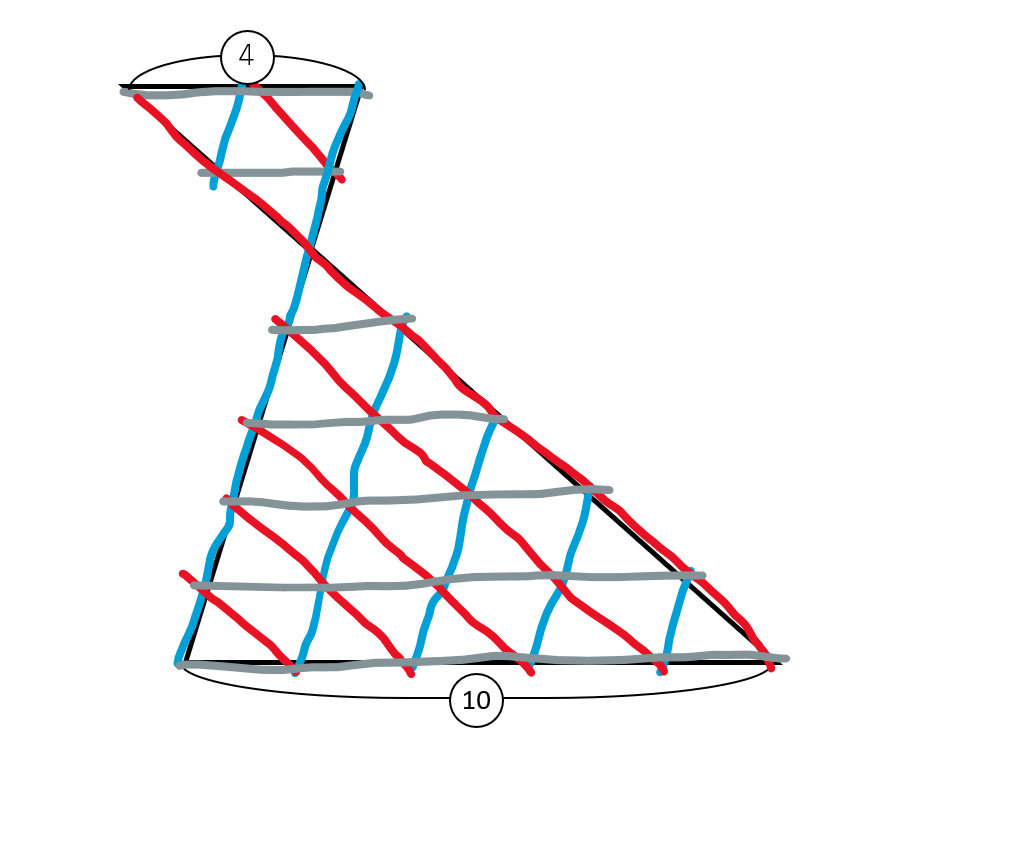
それでは、4cmと10cm、どちらも敷きつめられる大きさの
ちょっと小さなタイルを用意しましょう。

底辺が2cm、つまりアに4枚敷きつめられるタイルです。
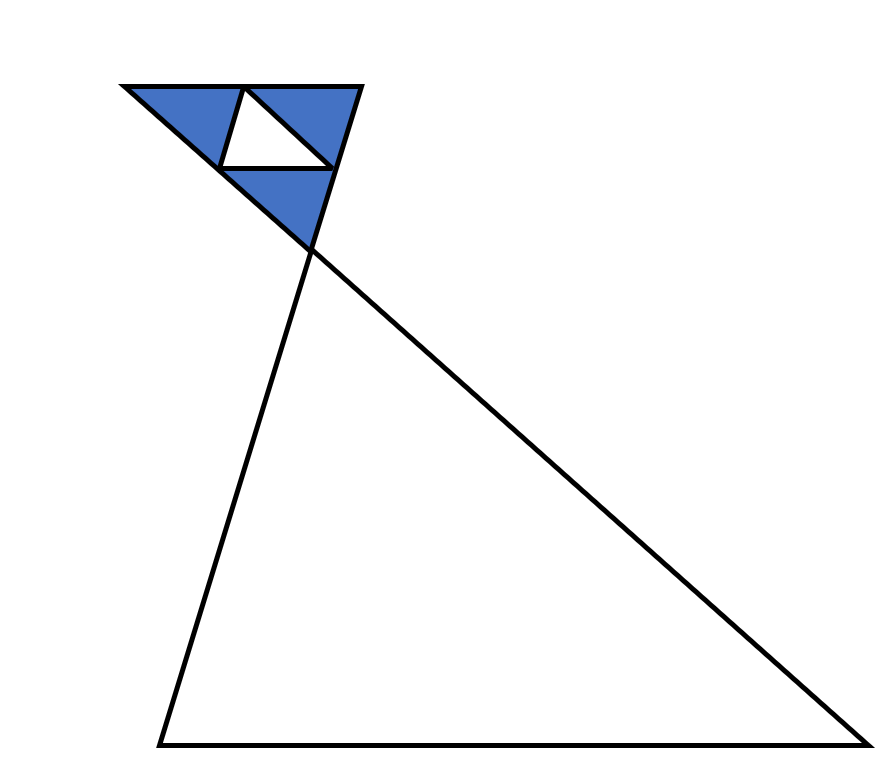
上記のタイルをたくさん使ってイにも敷きつめる、
というイメージです。
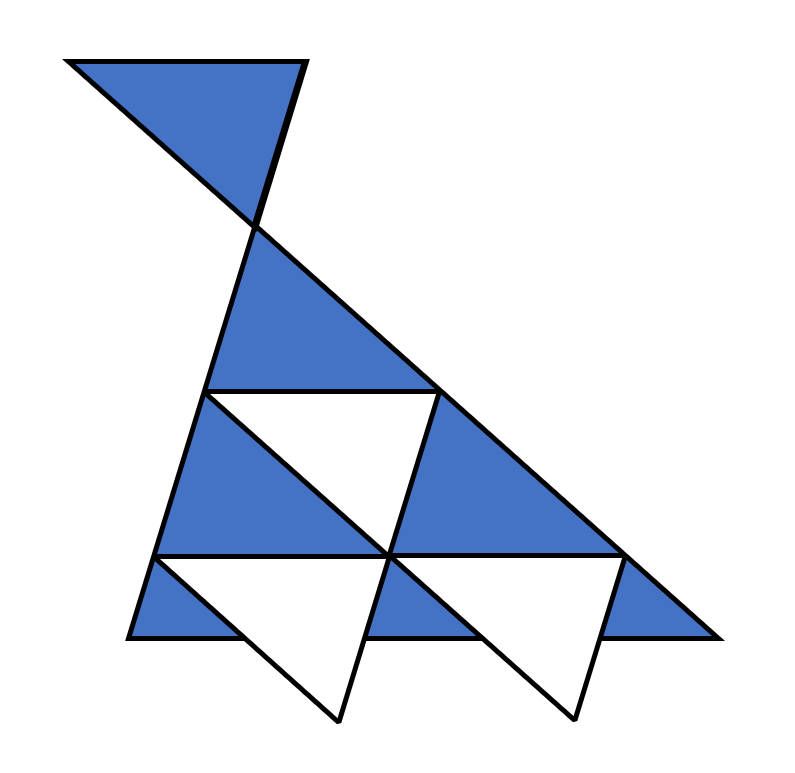
そうすると、こうなります。

どうでしょう?
アの部分にはタイルが4枚、イの部分にはタイルが25枚敷きつめられますね!
アには底辺2cmのタイルが2×2の4枚、イには底辺2cmのタイルが5×5の25枚
ということです。
補助線を引く感覚で、同じタイルを敷きつめていく…というイメージを持つと
わかりやすいと思います!
つまり、ア:イの面積比は$4:25$ということになります。
線を引いて考えてみよう!
たぶん、図形の問題を解く時には、辺のところに
①とか1⃣とか書き込むと思いますが、その感じで
ぜひぜひその図形を分解する、小さなタイルを
たくさん作る感じの補助線を引いてみてください。
それぞれの辺に平行な感じの線を描いてみましょう。
そうすることでとても分かりやすくなりますよ。
これまで絵や図をあまり描いたことがなければ、
線をひいたりするのはなかなか難しいかもしれません。
が、慣れれば慣れるほど図形の問題も解きやすくなります!
また、手を動かすことは
頭の中で仮説を立てたりイメージを持つことにとても役立つので
いいと思いますよ!
具体的なイメージを持つことが納得と理解につながる。
プロ家庭教師として、生徒さんにしっかり理解をしてもらえるよう
尽力していきます。
お気軽にご連絡ください。
お問い合わせ
☏電話でのお問い合わせ、
ご質問・ご相談はこちら
TEL.080-9895-5442
受付時間 / 9:30 – 21:00
※出られない場合は、折り返しお電話いたします
✉メールでのお問い合わせも受け付けています。








この記事へのコメントはありません。