京都（伏見・宇治）の家庭教師 | プロ家庭教師の内藤

中学受験、これだけは！時間の計算

こんにちは。京都（宇治・伏見）のプロ家庭教師　内藤　睦です。
ブログにご訪問いただき、ありがとうございます。
私の自己紹介はこちらから☟クリックして頂くと詳細に続きます。

こんにちは。
今日は中学受験する際にどうしても避けられない算数のポイント
時間の単位換算について書きたいと思います。

---

時間の単位換算とは？

---

難しい書き方をしていますが、ようは
「1時間は何分？」「1分30秒は何秒？」というように
同じ時間を単位を変えて表すことです。

算数の問題では、小学校2年生頃から
「1cm＝10mm」のように、長さを変える問題が出てきます。
長さや重さは、単位変換のルールを知っていたら
比較的やさしいのではないかと思います。

でも、時間は「1分＝60秒」「1時間＝60分」「1日＝24時間」
というように、10進法でないところがポイントです。
なので、「1時間＝60分」とわかっていても、
「9時間＝900分？」というような勘違いが出る場合は要注意です。

そして中学受験になると、これがさらに
「30分＝□時間」「24秒＝□分」といった
「小さい単位から大きい単位に変えると1未満になる」
変換をたくさんしなければいけません。
「120分＝□時間」なら簡単にできるけれど、
「45分＝□時間」と言われるとすぐピンと来ない、という
場合はどうするか？


たくさんの生徒さんを指導してきた上で、考えられる対策は3つです。
①理屈で考える
②イメージで考える
③暗記で乗り切る
それでは見ていきましょう。

---

①理屈で考える（対象者：しっかり考える力を身に着けたい人）

---

まずは、しっかり理屈を理解する方法です。
大変かもしれませんが、一番納得できて忘れにくい習得法だと思います。

前提として、「アナログ時計をイメージしながら考える」のが大切です。
なので、できればおもちゃの時計や針をいじってもいい時計が手元にあるといいでしょう。

あらためて、$1$分は1時間を何等分したものか、を考えてみましょう。
はい、$1$時間が$60$分ということは、$1$時間を$60$等分したもの、と考えることです。

そうすると、$1$分は$\dfrac{1}{60}$時間だということが分かりやすいと思います。

そしたら、こんどは$3$分は「 $\dfrac{1}{60}$時間が3つ集まったもの 」
と意識するようにしてみましょう。
そうすれば、「 $3$分＝$\dfrac{3}{60}$時間」がとてもわかりやすくなると思います。

その調子で「 $4$分＝$\dfrac{4}{60}$時間、つまり＝$\dfrac{1}{15}$時間」
という感じで約分していきましょう。割と約分ができる場合が多いので、注意が必要です。

---

②イメージで考える

---

これもアナログ時計を活用するやり方です。
「$30$分は何時間でしょうか」と尋ねられたら
こんなイメージがわくのではないでしょうか。

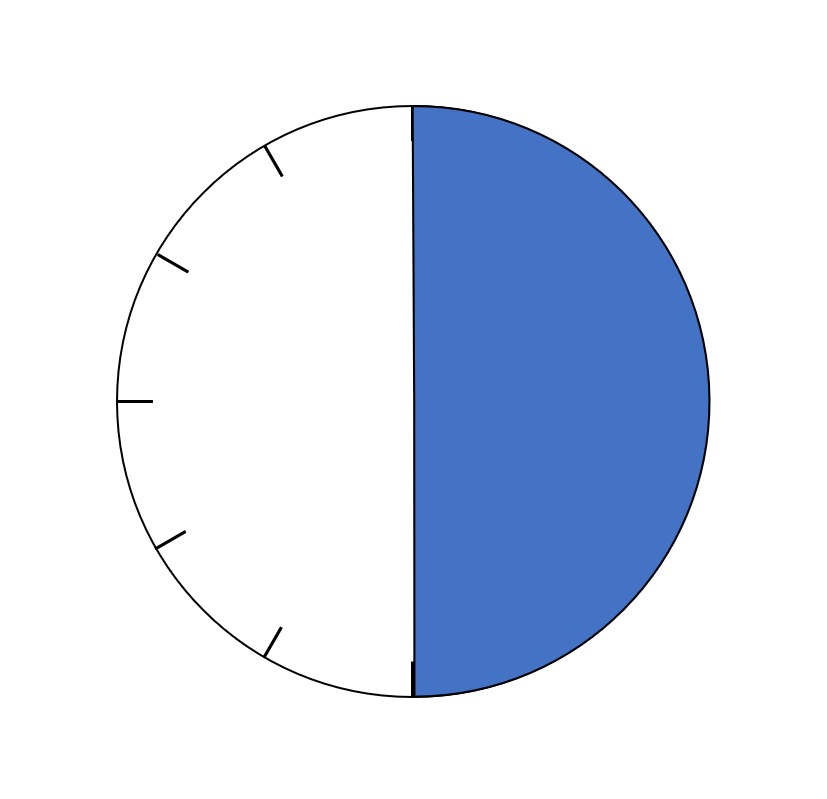
そう、時計のつくる円の半分。「〇時0分」から「〇時30分」まで針が動く感じですね。
これが2つ集まったらまるまる一つの円になることが分かると思います。
ということは、これは$\dfrac{1}{2}$時間ですね。

ではこれがさらに半分になったら？

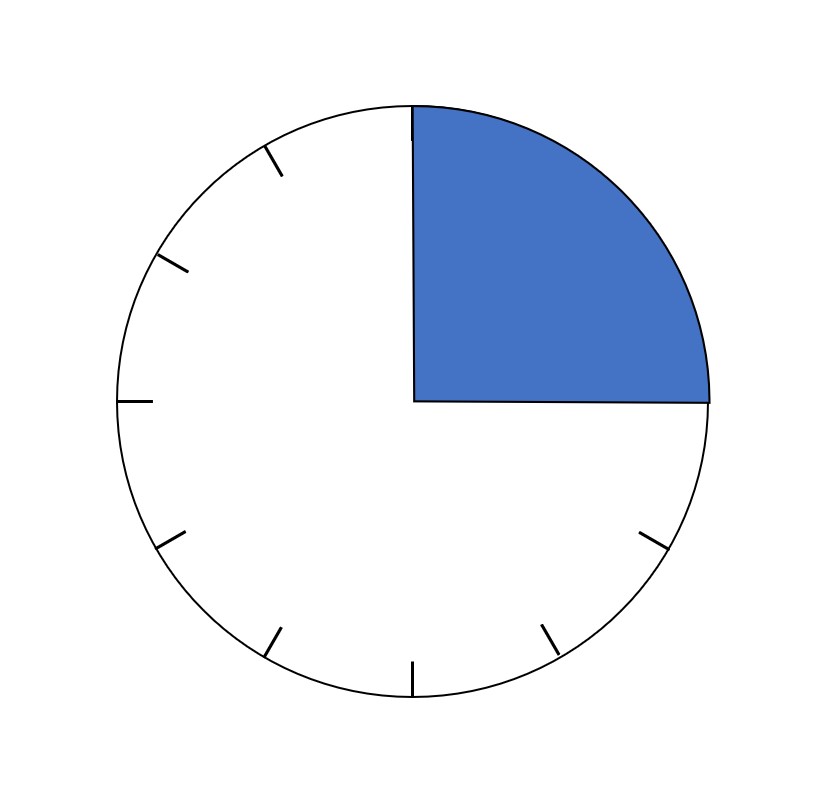
そうですね。これは四等分されているので、$\dfrac{1}{4}$時間です。
時間としては〇時ちょっきりから〇時15分」というイメージが持てるのではないでしょうか。
同じ形を四等分しているような感じですからね。
つまり、「 $15$分＝$\dfrac{1}{4}$時間、つまり＝$\dfrac{1}{4}$時間」
と理解する感じです。

同じ感じでこんなイメージを持つことができたらこちらのものです。

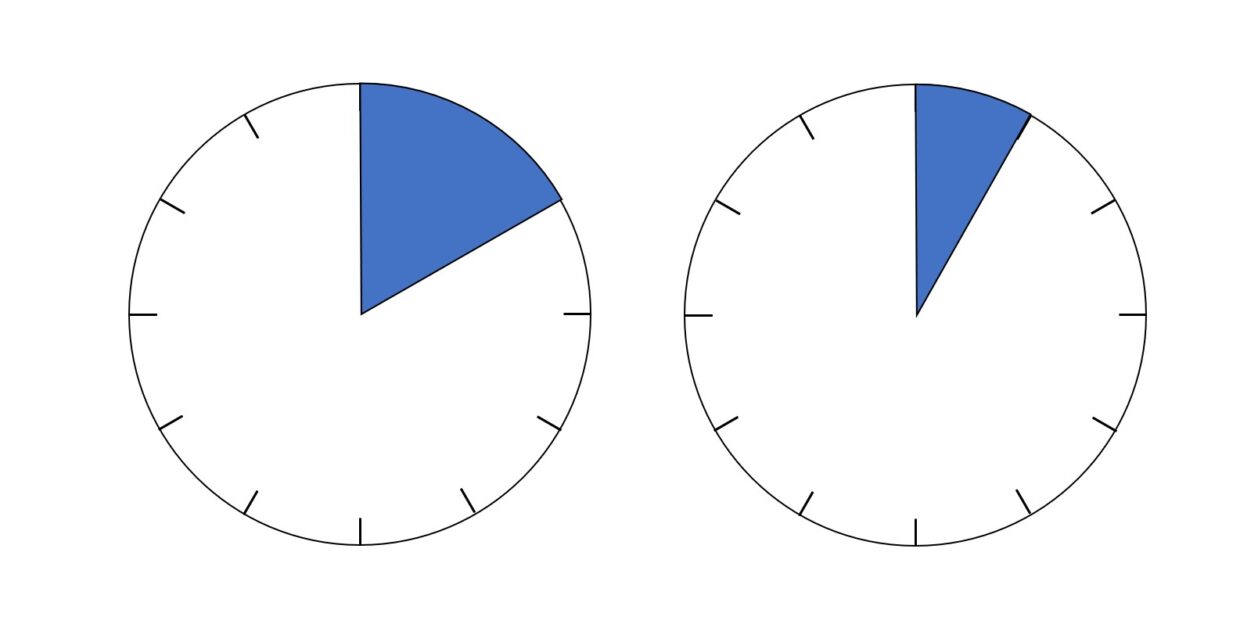
左側は10分ぶんで$10$分＝$\dfrac{1}{6}$時間、
右は5分ぶんで$5$分＝$\dfrac{1}{12}$時間
になります。
こんな感じで、ピザ1枚をピースに全部分けてまた新しく合ったら配布資料を1枚にする、
というような感覚で分数を伝えると、わかりやすくなると思います。

---

③暗記で乗り切る

---

「うーん、算数は考え方が難しい！」「算数はやっぱり嫌い」と悩んでおられる方
には、最終手段として「暗記」をやりましょう。
さっきの$1$分は$\dfrac{1}{60}$時間を利用ながら暗記しましょう。

どうでしょうか？
問題集を解く時は、表に載っているような単位換算が
たくさん出てきますが、おそらくランダムになっているでしょう。
添付ファイルのように、順番だったら暗記も難しくないのでは？と思います。

いかがでしたでしょうか？
理屈で深く分かるタイプ、暗記ができるタイプなど
それぞれのタイプに分けて、考え方や解き方を身に着けられるといいですね

分を時間で表す、といった内容は小学校4年生で出てきます。
中学受験では、速さの問題でももうはや必須です。
何かの形で、お子さまの記憶にすっかり残るようにすることが大切ですね！


もし単位換算でつまづきが発生しているなら
何かお困りの時は、ぜひお気軽にご相談ください！！